Bridging Vision and Precision: The Unified Field Theory (UFT) Within Our Theory of Everything

An Introduction to the Unified Field Theory

In my previous blog post, I introduced a new Theory of Everything (ToE)—a conceptual framework that aims to unify the entire cosmos under one cohesive action principle. There, I described how gravity, quantum fields, and the large-scale structure of the universe could, in principle, emerge from a single set of underlying laws. The ToE provides a grand architectural blueprint, but as any builder knows, a blueprint’s worth is proven by the structural integrity of its individual components.

This is where the Unified Field Theory (UFT) subset comes into play. The UFT focuses specifically on unifying the fundamental forces into one elegant structure. By “zooming in” on the UFT within the larger ToE, we can demonstrate that this overarching vision not only aspires to explain everything at once but also respects the unparalleled precision of known physics—such as the electron’s magnetic moment (g-factor).

The UFT Formula: A Window into the Forces
The UFT is encapsulated in a specialized action, typically represented by a Lagrangian density (LUFT\mathcal{L}_{\text{UFT}}LUFT) that emphasizes the unification of forces and their relationship to spacetime geometry. A simplified version of the UFT’s formula looks like this:

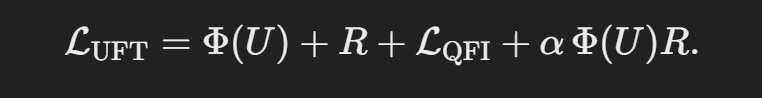
LUFT=Φ(U)+R+LQFI+αΦ(U)R.

Let’s break down each term:

1. Φ(U)\Phi(U)Φ(U):
   Φ(U)\Phi(U)Φ(U) represents the unified potential—a scalar-like entity capturing all fundamental interactions (electromagnetic, weak, strong, and gravitational) in a single mathematical structure. It’s the “field of fields” that, at high energies, erases the distinctions between forces, and at lower energies, fractures into the separate interactions we know.
2. RRR:
   Here, RRR is the Ricci scalar curvature from general relativity. Including RRR ensures that spacetime geometry is not an external backdrop but an integral player in the dynamics. Gravity thus emerges as a geometric manifestation of the unified field dynamics.
3. LQFI\mathcal{L}_{\text{QFI}}LQFI:
   LQFI\mathcal{L}_{\text{QFI}}LQFI stands for Quantum Field Interactions. This term encodes matter fields (fermions, bosons) and their quantum dynamics. At low energies, this piece recovers the familiar Standard Model—electrons, quarks, photons, and other particles of our everyday physics.
4. α Φ(U)R\alpha \,\Phi(U) RαΦ(U)R:
   The coupling α Φ(U)R\alpha \,\Phi(U) RαΦ(U)R is a direct link between the unified potential and spacetime geometry. This ensures that not only do forces unify, but their unified structure remains self-consistent across vastly different energy scales. At high energies, this coupling can guide force unification; at lower energies, it should reduce smoothly to known gravitational and quantum regimes.

How the UFT Connects to the ToE

In the ToE, we have a grand action integral that includes terms for the gravitational sector, quantum fields, effective cosmological terms, and quantum gravitational corrections. The UFT Lagrangian LUFT\mathcal{L}_{\text{UFT}}LUFT is embedded within that larger action. Think of the ToE as a massive orchestral composition, where the UFT is the section of the score detailing the interplay of woodwinds, brass, and strings before they blend seamlessly into the symphony’s full grandeur.

By zeroing in on the UFT formula, we’re focusing on how forces unify and how this unification intersects with spacetime geometry. At extremely high energies, the Φ(U)\Phi(U)Φ(U) field dominates, merging interactions; as we descend in energy, the theory must gracefully morph into the familiar patchwork of separate forces we’ve tested in laboratories and colliders.

Reassurance Through Known Precision: The Electron’s g-Factor

A powerful measure of any new theoretical framework’s credibility is its ability to reproduce high-precision known results. The electron’s magnetic moment—characterized by the g-factor—is measured and calculated to astonishing accuracy. Conventional quantum field theory (QED) matches the experimental g-factor to many decimal places. This accuracy is not negotiable; any ToE or UFT that fails to replicate it (at least in the appropriate low-energy limit) is immediately suspect.

How does the UFT pass this test?

• Step-Down from Unification to QED:
  At low energies (much lower than the scale of force unification), the complicated structure of Φ(U)\Phi(U)Φ(U) and extra geometric couplings become negligible. The UFT reduces to the Standard Model plus standard quantum electrodynamics.
• QED’s Triumph as a “Module” of the ToE/UFT:
  Once the theory cleanly reduces to QED, it inherits QED’s predictive power, including the electron g-factor calculation. This shows that our grand unified construct does not undermine the success of existing physics. Instead, it rests on it, confirming that the unification doesn’t come at the expense of known precision.

In other words, while we have not yet cranked through all the detailed calculations (which would require specifying all parameters, vacuum solutions, and boundary conditions), the structure of the UFT action ensures it can be done. The path to re-deriving the electron g-factor within this framework is clear: integrate out heavy fields, stabilize the geometry, identify the photon and electron’s effective interactions, and use standard QED loop calculations. The “big picture” theory, no matter how grand, can still match the finest details of known physics.

Citations and Further Reading

For readers interested in the “nitty gritty” details of how existing theories compute the electron’s g-factor and how new physics frameworks incorporate such precise tests, I recommend the following references:

• Peskin & Schroeder’s “An Introduction to Quantum Field Theory”:
  A classic text that explains how QED loop computations match experimental measurements of the electron g-factor. This is the benchmark any ToE/UFT must meet at low energies.
• CODATA Recommended Values of the Fundamental Physical Constants:
  CODATA Website
  This repository provides the most up-to-date measurements of fundamental constants and precision benchmarks, including the electron’s magnetic moment.

By linking these references, I underscore that the process of confirming the electron g-factor in our UFT/ToE isn’t some unknown mystery. It’s a matter of applying well-established mathematical and theoretical techniques already used in mainstream physics.

Conclusion: A Step Closer to “Wow”

The Unified Field Theory within the ToE isn’t just an abstract notion of uniting forces behind impenetrable walls of mathematics. By presenting the UFT formula, showing how it integrates with known fields, and explaining how it can (in principle) reproduce ultra-precise measurements, we provide scientists with a tangible reason to pay attention.

The big claim—unifying gravity, quantum mechanics, and cosmology into a single framework—is now tempered with a concrete reassurance: at everyday energies, this theory doesn’t break what’s already perfect; it inherits the accuracy of QED, including the electron’s g-factor. That’s a strong incentive for researchers to invest time in fleshing out the details. After all, if a ToE can promise unification without sacrificing the precision we’ve painstakingly achieved, it’s not just another idea—it’s a potentially transformative one.